BVH

The BVH functionality is encapsulated in the namespace EBGeometry::BVH. For the full API, see the doxygen API. There are two types of BVHs supported.

Full BVHs where the nodes are stored in build order and contain references to their children.
Compact BVHs where the nodes are stored in depth-first order and contain index offsets to children and primitives.

The full BVH is encapsulated by a class

template <class T, class P, class BV, size_t K>
class NodeT;

The above template parameters are:

T Floating-point precision.
P Primitive type to be partitioned.
BV Bounding volume type.
K BVH degree. K=2 will yield a binary tree, K=3 yields a tertiary tree and so on.

NodeT describes regular and leaf nodes in the BVH, and has member functions for setting primitives, bounding volumes, and so on. Importantly, NodeT is the BVH builder node, i.e. it is the class through which we recursively build the BVH, see Construction. The compact BVH is discussed below in Compact form.

Bounding volumes

EBGeometry supports the following bounding volumes, which are defined in EBGeometry_BoundingVolumes.hpp:

BoundingSphere, templated as EBGeometry::BoundingVolumes::BoundingSphereT<T> and describes a bounding sphere. Various constructors are available.
Axis-aligned bounding box, which is templated as EBGeometry::BoundingVolumes::AABBT<T>.

For full API details, see the doxygen API. Other types of bounding volumes can in principle be added, with the only requirement being that they conform to the same interface as the AABB and BoundingSphere volumes.

Construction

Constructing a BVH is done by:

Creating a root node and providing it with the geometric primitives and their bounding volumes.
Partitioning the BVH by providing a partitioning function.

The first step is usually a matter of simply constructing the root node using the full constructor, which takes a list of primitives and their associated bounding volumes. The second step is to recursively build the BVH. We currently support top-down and bottom-up construction (using space-filling curves).

Tip

The default construction methods performs the hierarchical subdivision by only considering the bounding volumes. Consequently, the build process is identical regardless of what type of primitives (e.g., triangles or analytic spheres) are contained in the BVH.

Top-down construction

Top-down construction is done through the function topDownSortAndPartition(), see the doxygen API for the BVH implementation.

The optional input arguments to topDownSortAndPartition are polymorphic functions of type indicated above, and have the following responsibilities:

PartitionerT is the partitioner function when splitting a leaf node into K new leaves. The function takes a list of primitives which it partitions into K new lists of primitives.
StopFunctionT simply takes a NodeT as input argument and determines if the node should be partitioned further.

Default arguments for these are provided, bubt users are free to partition their BVHs in their own way should they choose.

Bottom-up construction

The bottom-up construction uses a space-filling curve (e.g., a Morton curve) for first building the leaf nodes. This construction is done such that each leaf node contains approximately the number of primitives, and all leaf nodes exist on the same level. To use bottom-up construction, one may use the member function

    /*!
      @brief Function for doing bottom-up construction using a specified space-filling curve.
      @details The template parameter is the space-filling curve type. This function will partition the BVH
      by first sorting the bounding volume centroids along the space-filling curve. The tree is then constructed
      by placing at least K primitives in each leaf, and the leaves are then merged upwards until we reach the
      root node.
      @note S must have an encode and decode function which returns an SFC index. See the SFC namespace for
      examples for Morton and Nested indices. 
    */
    template <typename S>
    inline void
    bottomUpSortAndPartition() noexcept;

The template argument is the space-filling curve that the user wants to apply. Currently, we support Morton codes and nested indices. For Morton curves, one would e.g. call bottomUpSortAndPartition<SFC::Morton> while for nested indices (which are not recommended) the signature is likewise bottomUpSortAndPartition<SFC::Nested.

Build times for SFC-based bottom-up construction are generally speaking faster than top-down construction, but tends to produce worse trees such that traversal becomes slower.

Compact form

In addition to the standard BVH node NodeT<T, P, BV, K>, EBGeometry provides a more compact formulation of the BVH hierarchy where the nodes are stored in depth-first order. The “linearized” BVH can be automatically constructed from the standard BVH but not vice versa.

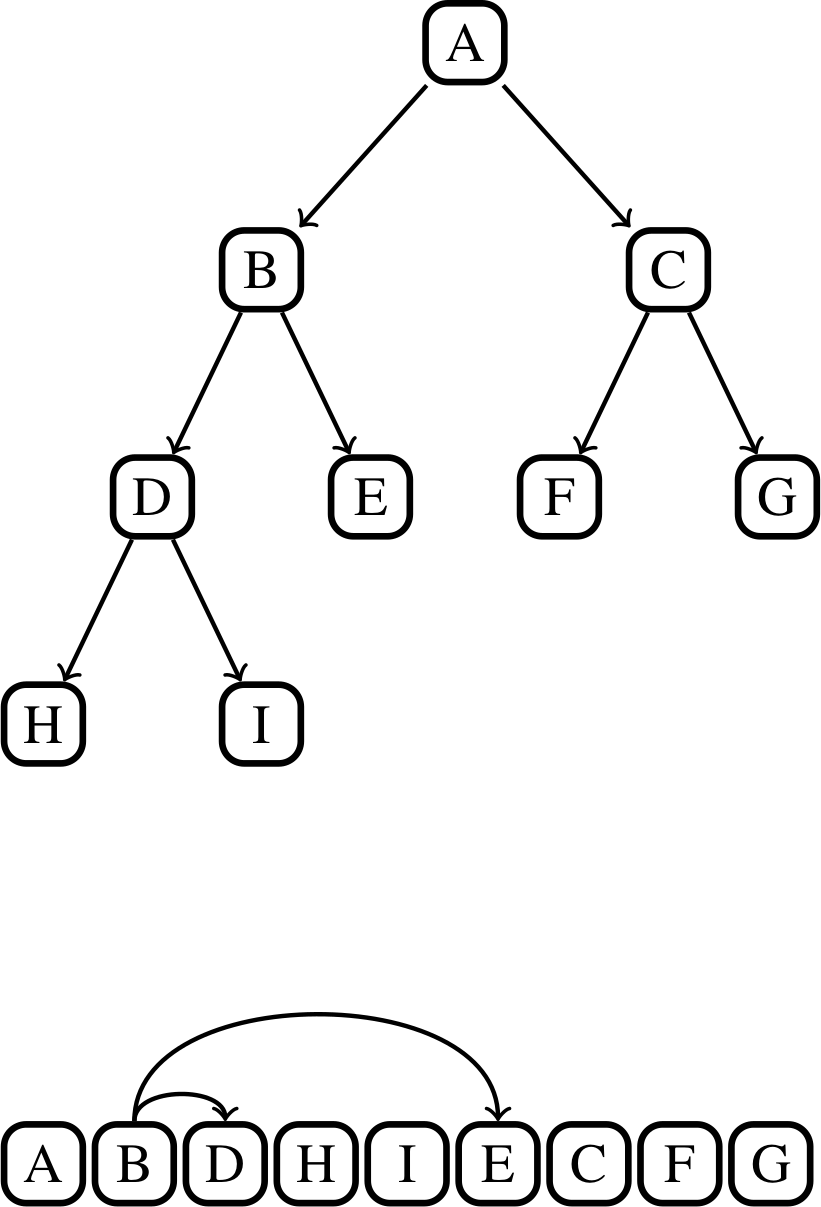
_images/CompactBVH.png — Fig. 6 Compact BVH representation. The original BVH is traversed from top-to-bottom along the branches and laid out in linear memory. Each interior node gets a reference (index offset) to their children nodes.

The rationale for reorganizing the BVH in compact form is it’s tighter memory footprint and depth-first ordering which occasionally allows a more efficient traversal downwards in the BVH tree, particularly if the geometric primitives are sorted in the same order. To encapsulate the compact BVH we provide two classes:

LinearNodeT which encapsulates a node, but rather than storing the primitives and pointers to child nodes it stores offsets along the 1D arrays. Just like NodeT the class is templated:
```
template <class T, class P, class BV, size_t K>
class LinearNodeT
```
LinearNodeT has a smaller memory footprint and should fit in one CPU word in floating-point precision and two CPU words in double point precision. The performance benefits of further memory alignment have not been investigated.

Note that LinearNodeT only stores offsets to child nodes and primitives, which are assumed to be stored (somewhere) as
```
std::vector<std::shared_ptr<LinearNodeT<T, P, BV, K> > > linearNodes;
std::vector<std::shared_ptr<const P> > primitives;
```
Thus, for a given node we can check if it is a leaf node (m_numPrimitives > 0) and if it is we can get the children through the m_childOffsets array. Primitives can likewise be obtained; they are stored in the primitives array from index m_primitivesOffset to m_primitivesOffset + m_numPrimities - 1.
LinearBVH which stores the compact BVH and primitives as class members. That is, LinearBVH contains the nodes and primitives as class members.
```
template <class T, class P, class BV, size_t K>
class LinearBVH
{
public:

protected:

  std::vector<std::shared_ptr<const LinearNodeT<T, P, BV, K>>> m_linearNodes;
  std::vector<std::shared_ptr<const P>> m_primitives;
};
```
The root node is, of course, found at the front of the m_linearNodes vector. Note that the list of primitives m_primitives is stored in the order in which the leaf nodes appear in m_linearNodes.

Constructing the compact BVH is simply a matter of letting NodeT aggregate the nodes and primitives into arrays, and return a LinearBVH. This is done by calling the NodeT member function flattenTree():

template <class T, class P, class BV, size_t K>
class NodeT
{
public:

  inline std::shared_ptr<LinearBVH<T, P, BV, K>>
  flattenTree() const noexcept;
};

which returns a pointer to a LinearBVH. For example:

// Assume that we have built the conventional BVH already
std::shared_ptr<EBGeometry::BVH::NodeT<T, P, BV, K> > builderBVH;

// Flatten the tree.
std::shared_ptr<LinearBVH> compactBVH = builderBVH->flattenTree();

// Release the original BVH.
builderBVH = nullptr;

Warning

When calling flattenTree, the original BVH tree is not destroyed. To release the memory, deallocate the original BVH tree. E.g., the set pointer to the root node to nullptr or ensure correct scoping.

Tree traversal

Both NodeT (full BVH) and LinearBVH (flattened BVH) include routines for traversing the BVH with user-specified criteria. For both BVH representations, tree traversal is done using a routine

template <class Meta>
inline void
traverse(const BVH::Updater<P>&                    a_updater,
         const BVH::Visiter<LinearNode, Meta>&     a_visiter,
         const BVH::Sorter<LinearNode, Meta, K>&   a_sorter,
         const BVH::MetaUpdater<LinearNode, Meta>& a_metaUpdater) const noexcept;

The BVH trees use a stack-based traversal pattern based on visit-sort rules supplied by the user.

Node visit

Here, a_visiter is a lambda function for determining if the node/subtree should be investigated or pruned from the traversal. This function has a signature

template <class NodeType, class Meta>
using Visiter = std::function<bool(const NodeType& a_node, const Meta a_meta)>;

where NodeType is the type of node (which is different for full/flat BVHs), and the Meta template parameter is discussed below. If this function returns true, the node will be visisted and if the function returns false then the node will be pruned from the tree traversal. Typically, the Meta parameter will contain the necessary information that determines whether or not to visit the subtree.

Traversal pattern

If a subtree is visited in the traversal, there is a question of which of the child nodes to visit first. The a_sorter argument determines the order by letting the user sort the nodes based on order of importance. Note that a correct visitation pattern can yield large performance benefits. The user is given the option to sort the child nodes based on what he/she thinks is a good order, which is done by supplying a lambda which sorts the children. This function has the signature:

template <class NodeType, class Meta, size_t K>
using Sorter = std::function<void(std::array<std::pair<std::shared_ptr<const NodeType>, Meta>, K>& a_children)>;

Sorting the child nodes is completely optional. The user can leave this function empty if it does not matter which subtrees are visited first.

Update rule

If a leaf node is visited in the traversal, distance or other types of queries to the geometric primitive(s) in the nodes are usually made. These are done by a user-supplied update-rule:

template <class P>
using Updater = std::function<void(const PrimitiveListT<P>& a_primitives)>;

Typically, the Updater will modify parameters that appear in a local scope outside of the tree traversal (e.g. updating the minimum distance to a DCEL mesh).

Meta-data

During the traversal, it might be necessary to compute meta-data that is helpful during the traversal, and this meta-data is attached to each node that is queried. This meta-data is usually, but not necessarily, equal to the distance to the nodes’ bounding volumes. The signature for meta-data construction is

template <class NodeType, class Meta>
using MetaUpdater = std::function<Meta(const NodeType& a_node)>;

The biggest difference between Updater and MetaUpdater is that Updater is only called on leaf nodes whereas MetaUpdater is also called for internal nodes. One typical example for DCEL meshes is that Updater computes the distance from an input point to the triangles in a leaf node, whereas MetaUpdater computes the distance from the input point to the bounding volumes of a child nodes. This information is then used in Sorter in order to determine a preferred child visit pattern when descending along subtrees.

Traversal algorithm

The code-block below shows the implementation of the BVH traversal. The implementation uses a non-recursive queue-based formulation when descending along subtrees. Observe that each entry in the stack contains both the node itself and any meta-data we want to attach to the node. If the traversal decides to visit a node, it immediately computes the specified meta-data of the node, and the user can then sort the children based on that data.

Listing 1 Tree traversal algorithm for the BVH tree.

  template <class T, class P, class BV, size_t K>
  template <class Meta>
  inline void
  NodeT<T, P, BV, K>::traverse(const BVH::Updater<P>&              a_updater,
                               const BVH::Visiter<Node, Meta>&     a_visiter,
                               const BVH::Sorter<Node, Meta, K>&   a_sorter,
                               const BVH::MetaUpdater<Node, Meta>& a_metaUpdater) const noexcept
  {
    std::array<std::pair<std::shared_ptr<const Node>, Meta>, K> children;
    std::stack<std::pair<std::shared_ptr<const Node>, Meta>>    q;

    q.emplace(this->shared_from_this(), a_metaUpdater(*this));

    while (!(q.empty())) {
      const auto& node = q.top().first;
      const auto& meta = q.top().second;

      q.pop();

      if (a_visiter(*node, meta)) {
        if (node->isLeaf()) {
          a_updater(node->getPrimitives());
        }
        else {
          for (size_t k = 0; k < K; k++) {
            children[k].first  = node->getChildren()[k];
            children[k].second = a_metaUpdater(*children[k].first);
          }

          // User-based visit pattern.
          a_sorter(children);

          for (const auto& child : children) {
            q.push(child);
          }
        }
      }
    }

Traversal examples

Below, we consider two examples for BVH traversal. The examples show how we compute the signed distance from a DCEL mesh, and how to perform a smooth CSG union where the search for the two closest objects is done by BVH traversal.

Signed distance

The DCEL mesh distance fields use a traversal pattern based on

Only visit bounding volumes that are closer than the minimum distance computed (so far).
When visiting a subtree, investigate the closest bounding volume first.
When visiting a leaf node, check if the primitives are closer than the minimum distance computed so far.

These rules are given below.

Listing 2 Tree traversal criterion for computing the signed distance to a DCEL mesh using the BVH accelerator. See Source/EBGeometry_MeshDistanceFunctionsImplem.hpp for details.

template <class T, class Meta, class BV, size_t K>
T
FastMeshSDF<T, Meta, BV, K>::signedDistance(const Vec3T<T>& a_point) const noexcept
{
  T minDist = std::numeric_limits<T>::infinity();

  BVH::Updater<Face> updater = [&minDist,
                                &a_point](const std::vector<std::shared_ptr<const Face>>& faces) noexcept -> void {
    for (const auto& f : faces) {
      const T curDist = f->signedDistance(a_point);

      minDist = std::abs(curDist) < std::abs(minDist) ? curDist : minDist;
    }
  };

  BVH::Visiter<Node, T> visiter = [&minDist, &a_point](const Node& a_node, const T& a_bvDist) noexcept -> bool {
    return a_bvDist <= std::abs(minDist);
  };

  BVH::Sorter<Node, T, K> sorter =
    [&a_point](std::array<std::pair<std::shared_ptr<const Node>, T>, K>& a_leaves) noexcept -> void {
    std::sort(
      a_leaves.begin(),
      a_leaves.end(),
      [&a_point](const std::pair<std::shared_ptr<const Node>, T>& n1,
                 const std::pair<std::shared_ptr<const Node>, T>& n2) -> bool { return n1.second > n2.second; });
  };

  BVH::MetaUpdater<Node, T> metaUpdater = [&a_point](const Node& a_node) noexcept -> T {
    return a_node.getDistanceToBoundingVolume(a_point);
  };

  // Traverse the tree.
  m_bvh->traverse(updater, visiter, sorter, metaUpdater);

  return minDist;

CSG Union

Combinations of implicit functions in EBGeometry into aggregate objects can be done by means of CSG unions. One such union is known as the smooth union, in which the transition between two objects is gradual rather than abrupt. Below, we show the traversal code for this union, where we traverse through the tree and obtains the distance to the two closest objects rather than a single one.

Listing 3 Tree traversal when computing the smooth CSG union. See Source/EBGeometry_CSGImplem.hpp for details.

template <class T, class P, class BV, size_t K>
T
FastSmoothUnionIF<T, P, BV, K>::value(const Vec3T<T>& a_point) const noexcept
{
  // For the smoothed CSG union we use a smooth min operator on the two closest
  // primitives.

  // Closest and next closest primitives.
  T a = std::numeric_limits<T>::infinity();
  T b = std::numeric_limits<T>::infinity();

  BVH::Updater<P> updater =
    [&a, &b, &a_point](const std::vector<std::shared_ptr<const P>>& a_implicitFunctions) noexcept -> void {
    for (const auto& implicitFunction : a_implicitFunctions) {
      const auto& d = implicitFunction->value(a_point);

      if (d < a) {
        b = a;
        a = d;
      }
      else if (d < b) {
        b = d;
      }
    }
  };

  BVH::Visiter<Node, T> visiter = [&a, &b](const Node& a_node, const T& a_bvDist) noexcept -> bool {
    return a_bvDist <= 0.0 || a_bvDist <= a || a_bvDist <= b;
  };

  BVH::Sorter<Node, T, K> sorter =
    [&a_point](std::array<std::pair<std::shared_ptr<const Node>, T>, K>& a_leaves) noexcept -> void {
    std::sort(
      a_leaves.begin(),
      a_leaves.end(),
      [&a_point](const std::pair<std::shared_ptr<const Node>, T>& n1,
                 const std::pair<std::shared_ptr<const Node>, T>& n2) -> bool { return n1.second > n2.second; });
  };

  BVH::MetaUpdater<Node, T> metaUpdater = [&a_point](const Node& a_node) noexcept -> T {
    return a_node.getDistanceToBoundingVolume(a_point);
  };

  this->m_bvh->traverse(updater, visiter, sorter, metaUpdater);

  return m_smoothMin(a, b, m_smoothLen);
}